推荐学习书目
› Learn Python the Hard Way
Python Sites
› PyPI - Python Package Index
› http://diveintopython.org/toc/index.html
› Pocoo
值得关注的项目
› PyPy
› Celery
› Jinja2
› Read the Docs
› gevent
› pyenv
› virtualenv
› Stackless Python
› Beautiful Soup
› 结巴中文分词
› Green Unicorn
› Sentry
› Shovel
› Pyflakes
› pytest
Python 编程
› pep8 Checker
Styles
› PEP 8
› Google Python Style Guide
› Code Style from The Hitchhiker's Guide
这是一个创建于 3135 天前的主题,其中的信息可能已经有所发展或是发生改变。
我不是教你诈!玩的时候可以计算一下哦!
玩 21 点 大家都不陌生,今天兴致来临,和朋友搞了一个简单的基于凯利公式的 21 点 游戏仓位管理。可以试试。

凯利公式: f=p/rl-(1-p)/rwrw :赢赚比例 rl : 输赔比例 p : 赢概率 pf : 投注比例
可以通过自己是否为庄家调整输赢比例,还有输赢概率。
假设我的 rw = 100%rl = -100%p = 55%则最佳理论值 f 为:
rw = 1
rl = -1
p = 0.55
f = (p/abs(rl) -(1-p)/abs(rw))*100
print('则最佳理论值 f 为: &# 39; + '%0.2f&# 39;%(f) + '%&# 39;)
则最佳理论值 f 为: 10.00%
初始资产为 1000 元 ,模拟玩 一轮玩 1000 次 ,玩 9 轮
import random
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.style.use('ggplot&# 39;)
import seaborn as sns
from CAL.PyCAL import font
import random
def runOneTurnGame(rw, rl, p):
assets = [1000]
f=p/abs(rl)-(1-p)/abs(rw)
for i in range(1000):
lastAsset = assets[-1]
isWin = True if random.random() < p else False
if isWin:
currentAsset = lastAsset*(1-f) + lastAsset*f*(1+rw)
else:
currentAsset = lastAsset*(1-f) + lastAsset*f*(1+rl)
assets.append(currentAsset)
return assets
完整高清源代码,请移步: https://uqer.io/community/share/57bec81c228e5b79a675acf3
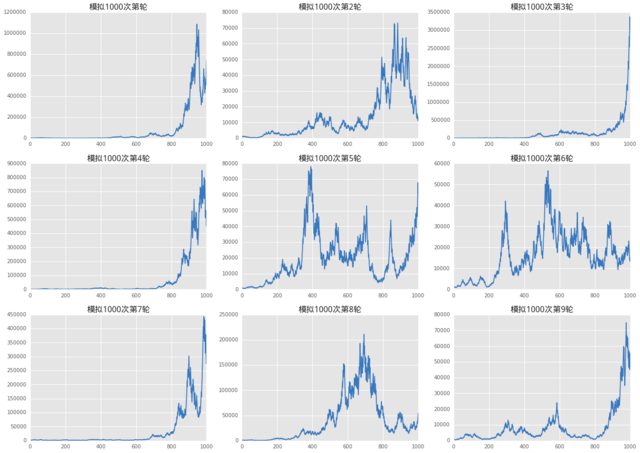
结论可以看出,结果大概有 4 种类型,但是,统计发现,在游戏中,中后局的胜率要比其他时间段高很多。玩的次数越多,胜率越大。还可以进行各种统计,这个大家自己可以总结。
玩 21 点 大家都不陌生,今天兴致来临,和朋友搞了一个简单的基于凯利公式的 21 点 游戏仓位管理。可以试试。

凯利公式: f=p/rl-(1-p)/rwrw :赢赚比例 rl : 输赔比例 p : 赢概率 pf : 投注比例
可以通过自己是否为庄家调整输赢比例,还有输赢概率。
假设我的 rw = 100%rl = -100%p = 55%则最佳理论值 f 为:
rw = 1
rl = -1
p = 0.55
f = (p/abs(rl) -(1-p)/abs(rw))*100
print('则最佳理论值 f 为: &# 39; + '%0.2f&# 39;%(f) + '%&# 39;)
则最佳理论值 f 为: 10.00%
初始资产为 1000 元 ,模拟玩 一轮玩 1000 次 ,玩 9 轮
import random
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.style.use('ggplot&# 39;)
import seaborn as sns
from CAL.PyCAL import font
import random
def runOneTurnGame(rw, rl, p):
assets = [1000]
f=p/abs(rl)-(1-p)/abs(rw)
for i in range(1000):
lastAsset = assets[-1]
isWin = True if random.random() < p else False
if isWin:
currentAsset = lastAsset*(1-f) + lastAsset*f*(1+rw)
else:
currentAsset = lastAsset*(1-f) + lastAsset*f*(1+rl)
assets.append(currentAsset)
return assets
完整高清源代码,请移步: https://uqer.io/community/share/57bec81c228e5b79a675acf3

结论可以看出,结果大概有 4 种类型,但是,统计发现,在游戏中,中后局的胜率要比其他时间段高很多。玩的次数越多,胜率越大。还可以进行各种统计,这个大家自己可以总结。
目前尚无回复