这是一个创建于 2936 天前的主题,其中的信息可能已经有所发展或是发生改变。
起因
在群里看到一道算法题 题目如下:
求 1<=i<=10**12 范围内所有 d(i)的和的末 12 位, d(i)表示 i 的正约数的和, i 为整数
因为我本人对非科班 算法导论买回来拿去垫杯子了(书:怪我咯) 就看了一点冒泡 桶排 快排 啥的 什么 leetcode 都没有刷过,纯粹小白。
当时想法很简单
- 数字很大,很多,排序我就用桶吧
- 自然数由 0 , 1 素数和合数构成 (小学课本写的。。) 后来我发现 合数可以由 多个乘积构成 也就是我要找到素数列表 然后组合成为所有 0-10**12 的自然数就好了
整理一下思路就是:
- 在遍历的过程中判断该数字是否为素数,是就放进素数列表,否就是合数,我需要写一个方法来解析这个合数
- 合数由多个素数的乘积构成比如 6=2^1 * 3^1 这样构成 因此可以通过遍历素数列表 看能否余数为零,为零我就在其基础上加一 变成{6 :{2:1,3:1,5:0}} 这样一个映射表
- 再循环过程中根据质数和定律自动计算并求和
现在面临的问题是:
- 跑到 10000 就需要 38 秒 这样算下来看起来需要到明年,这个算法还是很耿直
我看到知乎上有优化算法,期待大神能够帮我解释一下: 如图:
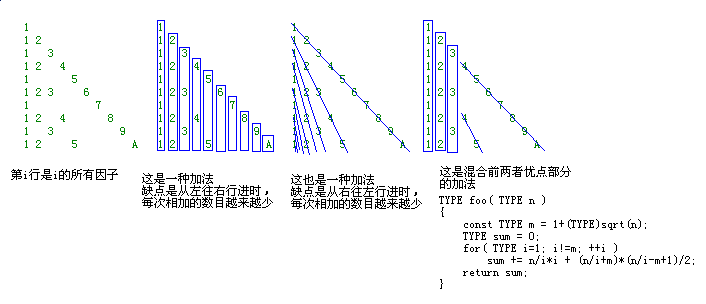

按图索骥好像看到这样一些结论:
在一个大于 1 的数 a 和它的 2 倍之间(即区间(a, 2a]中)必存在至少一个素数。
存在任意长度的素数等差数列。(格林和陶哲轩, 2004 年)
顺便说一下 现在进群的要求不低啊 开学我要回去拿回我的垫杯书 囧
1
Xs0ul 2017-01-25 23:55:43 +08:00 你的第一个图应该就能解释是怎么优化的,第二个图挂了不知道是啥。
证明反而麻烦,我就拿个例子来解释好了。方便说明,我把 i 的范围改成 1 ~ 4 (看懂了就知道 10^12 同理)。 约数有: 1 : 1 , 2 : 1 , 2 , 3 : 1 , 3 , 4 : 1 , 2 , 4 式子的第一项,求和方法是 (1) + (1 + 2) + (1 + 3) + (1 + 2 + 4) = 15 而优化的方法,也就是第二项 /第三项,求和方法是 (1 * 4) + (2 * 2) + (3 * 1) + (4 * 1) = 15 。乘法中左边是 1 ~ 4 ,右边是 [4 / i]。 归根结底,是改变了求和的顺序。实际上,所有 d 的倍数,在求和的时候都会被加一次(作为 1d 、 2d ……[10^12 / d]d 的约数),一共就是 [10^12 / d] 次。优化的方法好处就是,不必花时间去找约数,而求约数是相当费力的一件事。 |
2
mickeyandkaka 2017-01-26 00:00:40 +08:00 |
3
slysly759 OP @mickeyandkaka ~ ~ thx
|