这是一个创建于 2597 天前的主题,其中的信息可能已经有所发展或是发生改变。
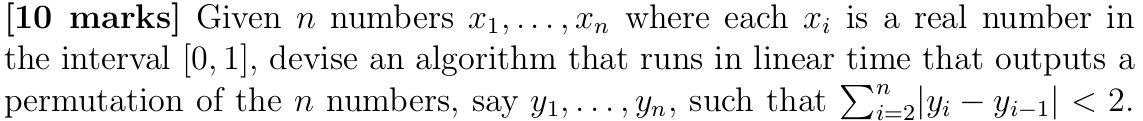 目前的想法是开一个 N 的 array 作为桶,遍历这 N 个数,每次拿这个数乘以 N 然后再取整,作为下标 idx。这个数就放入下标为 idx 的桶中。最后合并桶里的元素。
目前的想法是开一个 N 的 array 作为桶,遍历这 N 个数,每次拿这个数乘以 N 然后再取整,作为下标 idx。这个数就放入下标为 idx 的桶中。最后合并桶里的元素。
1
xml123 2018-03-10 14:03:38 +08:00 正确的。
首先在给定的序列中插入新的数不会使求和的式子变小,因为 |a-b|<=|a-c|+|c-b| 。 然后把你最后生成的数列按桶分成若干组(设有 m 个桶,m<=n ),每一组最后插入该组第一个数,下面证明修改后的序列满足不等式。 把求和分成两部分,y_i 和 y_i-1 在同一组里的,不在同一组里的。 同一组里的元素为分布在长度为 1/n 区间内的实数,任意两数之差绝对值小于 1/n,同一组 k 个数相邻元素差的绝对值之和小于(k-1)/n,由于一共有 n+m 个数,m 组,所以这些和小于 1。 不同组元素的差的绝对值之和可以看出等于第一个数与最后一个数差的绝对值,该值小于 1。 所以两部分之和小于 2。 (稍微修改证明过程可以证明和小于 2-2/n,应该是你给出的算法的上界了。) |
2
ytterbium 2018-03-10 14:41:43 +08:00 via Android 简单点说就是,每个桶 i 里差总和小于等于(k_i-1)/n,所有桶内和小于等于 sum{(k_i-1)/n}=(n-h)/n<1,h 是非空桶的个数。桶之间的差绝对值之和是在有序序列上算的,小于等于 1。所以两部分总和小于 2。
|
4
letianqiu OP |
5
ytterbium 2018-03-10 21:18:39 +08:00 via Android
桶数增大,由 n 换成 m,m>n,m 和 eplison 什么关系没想好,不过复杂度就是 O(m)了
|
6
ytterbium 2018-03-10 21:19:53 +08:00 via Android
题目说的线性复杂度,O(m)也是线性,还算符合要求吧
|
7
ytterbium 2018-03-10 21:21:34 +08:00 via Android
如果 m 可以写成 eplison 的表达式,就是关于 eplison 的线性算法,O(eplison)
|