推荐学习书目
› Learn Python the Hard Way
Python Sites
› PyPI - Python Package Index
› http://diveintopython.org/toc/index.html
› Pocoo
值得关注的项目
› PyPy
› Celery
› Jinja2
› Read the Docs
› gevent
› pyenv
› virtualenv
› Stackless Python
› Beautiful Soup
› 结巴中文分词
› Green Unicorn
› Sentry
› Shovel
› Pyflakes
› pytest
Python 编程
› pep8 Checker
Styles
› PEP 8
› Google Python Style Guide
› Code Style from The Hitchhiker's Guide
这是一个创建于 2206 天前的主题,其中的信息可能已经有所发展或是发生改变。
关于这个队列实现的版本中:
为什么每次要从队列中选取距离最小的顶点出发?而不是按照广度优先的顺序?
代码如下:
def dijkstra1(graph, start):
distances = {vertex: float('inf') for vertex in graph}
distances[start] = 0
visited = set()
queue = list(graph.keys())
while queue:
vertex = min(queue, key=lambda vertex: distances[vertex])
queue.remove(vertex)
visited.add(vertex)
for neighbor in graph[vertex]:
if distances[vertex] + graph[vertex][neighbor] < distances[neighbor]:
distances[neighbor] = distances[vertex] + graph[vertex][neighbor]
if neighbor not in visited:
queue.append(neighbor)
return distances
我试着用广度优先搜索,发现也不影响实际结果,而且性能和用最小堆实现的差不多
from collections import deque
def dijkstra2(graph, start):
distances = {vertex: float('inf') for vertex in graph}
distances[start] = 0
visited = set()
queue = deque([start])
while queue:
vertex = queue.popleft()
visited.add(vertex)
for neighbor in graph[vertex]:
if distances[vertex] + graph[vertex][neighbor] < distances[neighbor]:
distances[neighbor] = distances[vertex] + graph[vertex][neighbor]
if neighbor not in visited:
queue.append(neighbor)
return distances
测试代码
g = {
'A': {'B': 3, 'D': 1},
'B': {'A': 3, 'C': 5, 'D': 4, 'E': 5},
'C': {'B': 5, 'E': 9},
'D': {'A': 1, 'B': 4, 'E': 1},
'E': {'B': 5, 'C': 9, 'D': 1}
}
print(dijkstra(g, 'A'))
测试图
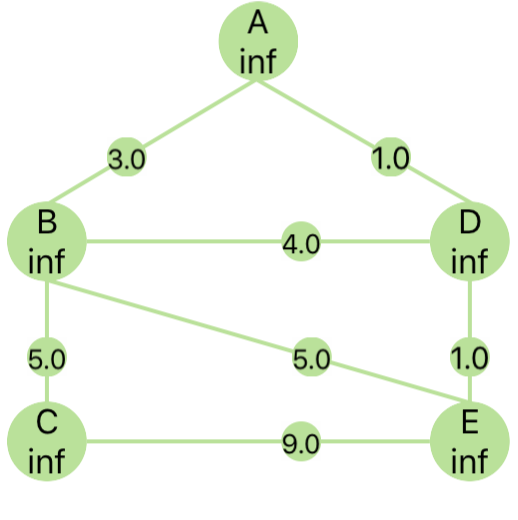
第 1 条附言 · 2019-02-23 22:44:30 +08:00
知道区别了,@66450146 说的队,如果不给定终点,两种方法计算所有的顶点是没有区别的。
但如果要计算起点指定终点的最短路径,我的 BFS 算法中,对于当前顶点,路径不一定是最短路径,需要访问完所有的顶点才能确定最短路径,而 Dijkstra 算法对于当前顶点,走的就是最短路径,不用计算所有顶点。
最终代码如下:
from heapq import heappush, heappop
def dijkstra(graph, source, destination=None):
distances = {vertex: float('inf') for vertex in graph}
distances[source] = 0
priority_queue = [(distances[source], source)]
precursors = {}
while priority_queue:
distance, vertex = heappop(priority_queue)
if distance == distances[vertex]:
if destination == vertex:
break
for neighbor in graph[vertex]:
if distances[vertex] + graph[vertex][neighbor] < distances[neighbor]:
distances[neighbor] = distances[vertex] + graph[vertex][neighbor]
heappush(priority_queue, (distances[neighbor], neighbor))
precursors[neighbor] = vertex
if destination:
precursor = destination
path = []
while precursor:
path.append(precursor)
precursor = precursors.get(precursor)
return distances[destination], path[::-1]
paths = []
for precursor in precursors:
path = []
while precursor:
path.append(precursor)
precursor = precursors.get(precursor)
paths.append(path[::-1])
return distances, paths
第 2 条附言 · 2019-02-24 02:33:32 +08:00
刚才看 Bellman-Ford 算法,才发现我写的 bfs 队列版本竟然和 SPFA 的思路是一样的,不过这里没有检测环路,因此对于只有正权边的图是适用的。
1
MrAMS 2019-02-23 20:05:50 +08:00
Dijkstra 本质上其实就是个贪心
每次要从队列中选取距离最小的顶点出发保证了每一步的最优 (广度优先搜索出来的,因为数据特殊?) |
3
Fulcrum 2019-02-23 20:13:56 +08:00 via Android
没记错是因为
P(n)+p(n+1)>=p(x)+p(n+1)?去年学的运筹,基本忘了。。。 是反证法证明的。 |
4
Fulcrum 2019-02-23 20:14:15 +08:00 via Android
没记错是因为
P(n)+p(n+1)>=p(x)+p(n+1)?去年学的运筹,基本忘了。。。 是反证法证明的,记得很短。 建议找本运筹学看看,有证明的 |
5
66450146 2019-02-23 21:15:26 +08:00 这是使用场景不合适,Dijkstra 更适合你只关心从 A->E 的距离,而不关心到其他节点距离的时候。具体的做法就是在中间提早 return,可以证出来 Dijkstra 得出的一定是最优解,而 BFS 的做法不一定
def dijkstra1(graph, start, end): distances = {vertex: float('inf') for vertex in graph} distances[start] = 0 visited = set() queue = list(graph.keys()) while queue: vertex = min(queue, key=lambda vertex: distances[vertex]) queue.remove(vertex) visited.add(vertex) for neighbor in graph[vertex]: if distances[vertex] + graph[vertex][neighbor] < distances[neighbor]: distances[neighbor] = distances[vertex] + graph[vertex][neighbor] if neighbor == end: return distances[neighbor] if neighbor not in visited: queue.append(neighbor) |
6
66450146 2019-02-23 21:16:52 +08:00
格式乱了,就是加了一个 if ... return 而已,两种做法对于:
g = { 'A': {'B': 1, 'F': 99}, 'B': {'A': 1, 'C': 1}, 'C': {'B': 1, 'D': 1}, 'D': {'C': 1, 'E': 1}, 'E': {'D': 1, 'F': 99}, 'F': {'A': 99, 'E': 99} } 得出来的结果是不一样的 |